【如图becd交于点a】如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED..._数学_gnr0473
编辑: admin 2017-15-06
-
4
检举|2011-03-28 15:18
(1)
∵ CF平分∠BCD,EF平分∠BED
∴ ∠1 = ∠2,∠3 =∠4
∵ 在△DME和△FMC中,有一对对顶角,即∠DME=∠FMC
∴ ∠D +∠1 = ∠F +∠3
又∵ 在△BNC和△FNE中,有一对对顶角,即∠BNC=∠FNE
∴ ∠B +∠4 = ∠F +∠2
∴ ∠D +∠1 +∠B +∠4 = ∠F +∠2+ ∠F +∠3 【以上 2式 相加】
∴ ∠D +∠B = 2∠F
(2)
∵ DE‖BC
∴ ∠B =∠BED = 2∠2
在△ABC中,∠B + 2∠4 + ∠BAC =180° 即 2∠2+ 2∠4 + ∠BAC =180°
∴ ∠2 + ∠4 =180° -80° =100°
又∵ ∠B +∠4 = ∠F +∠2
∴ ∠F = ∠2 +∠4 =100°
向左转|向右转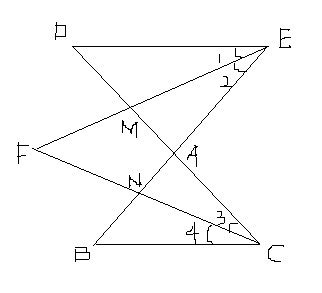
互助这道作业题的同学还参与了下面的作业题
题1: 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线(1)若∠B=30°,∠D=40°,求∠F=?(2)若∠B:∠D:∠F=2:4:x,求x的值[数学科目]
1)
因为CF为角BCD的平分线,EF为角BED的平分线
所以设∠FED=∠FEB=X,∠FCB=∠FCD=Y
则根据三角形内角和定理得:
X+∠D=Y+∠F
Y+∠B=X+∠F
两式相加得:
2∠F=∠B+∠D=30°+40°=70°
所以∠F=35°
2)
因为∠B:∠D:∠F=2:4:X
所以可设:∠B=2K,∠D=4K,∠F=X*K
因为
2∠F=∠B+∠D
所以
2*X*K=2K+4K
所以X=3
题2: 如图所示,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.(1)填空:∠5=∠1+(),∠5=∠2+(),∠6=∠B+(),∠6=∠F+();(2)将(1)中的∠5和∠6分别相加,你能说明2∠F=∠B+∠D吗?试[数学科目]
1、
∠5=∠1+(∠D),∠5=∠2+(∠F),∠6=∠B+(∠4),∠6=∠F+(∠3)
2、证明:
∵CF平分∠BCD
∴∠2=∠4
∴∠5=∠2+∠F=∠4+∠F
∵∠6=∠F+∠3
∴∠5+∠6=∠3+∠4+2∠F
∵EF平分∠BED
∴∠1=∠3
∴∠5=∠1+∠D=∠3+∠D
∵∠6=∠B+∠4
∴∠5+∠6=∠3+∠4+∠B+∠D
∴∠3+∠4+2∠F=∠3+∠4+∠B+∠D
∴2∠F=∠B+∠D
题3: 如图,BE与CD交于A,CF为∠BCD的平分线,EF为∠BED的平分线:(1)试探求∠F与∠B、∠D之间的关系(2)若∠B:∠D:∠F=2:4:x,求x的值[数学科目]
1、∠∠∠∠∠∠
∠F=(∠B+∠D)/2.证明如下:
知∠EAC=∠D+∠AED=∠B∠ACB,
则2∠EAC=∠D+∠AED+∠B+∠ACB,∠EAC=1/2∠D+1/2∠B+1/2∠AED+1/2∠ACB=∠AEF+∠ACF+1/2∠B+1/2∠D.
又知∠EAC=∠AEF+∠ACF+∠F,
所以∠F=(∠B+∠D)/2.
2、由上面结论得x=(2+4)/2=3.
题4: 【如图,BE,CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线试探求∠F与∠B、∠D之间的关系,并说明理由∠B:∠D:∠F=2:4:x,求x值图错了】[数学科目]
将CF与BE的交点定为M,将EF与CD的交点定为N
设∠BCF=∠1,∠DCF=∠2,∠BEF=∠3,∠DEF=∠4
1、
∵CF平分∠BCD
∴∠1=∠2
∴∠BCD=∠1+∠2=2∠1
∵EF平分∠BED
∴∠3=∠4
∴∠BED=∠3+∠4=2∠3
∵∠BAD=∠B+∠BCD=∠B+2∠1,∠BAD=∠D+∠BED=∠D+2∠3
∴∠B+2∠1=∠D+2∠3
∴∠1-∠3=(∠D-∠B)/2
∵∠CME=∠B+∠1,∠CME=∠F+∠3
∴∠B+∠1=∠F+∠3
∴∠1-∠3=∠F-∠B
∴∠F-∠B=(∠D-∠A)/2
∴∠F=∠B+(∠D-∠B)/2=(∠B+∠D)/2
∴∠B+∠D=2∠F
2、设∠B=2K
∵∠B:∠D:∠F=2:4:X,∠B=2K
∴∠D=4K,∠F=XK
∵∠B+∠D=2∠F
∴2K+4K=2XK
∴X=3
题5: 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的角平分线.若∠5=∠1+∠D、∠5=∠2+∠F;若∠6=∠B+∠4、∠6=∠F+∠3.说明2∠F=∠B+∠D.[数学科目]
∵∠5=∠2+∠F,∠6=∠F+∠3
∴∠5+∠6=2∠F+∠2+∠3
∴2∠F=∠5+∠6-∠2-∠3
又∵∠1=∠3,∠2=∠4,
∴2∠F=∠5+∠6-∠1-∠4
=(∠5-∠1)+(∠6-∠4)
又∵∠D=∠5-∠1,∠B=∠6-∠4,
∴2∠F=∠B+∠D
有疑问,请追问;若满意,请采纳.谢谢!
