【设a大于b大于0证明】【设a大于b大于0证明,(a-b)小于Ln(ab)小于[(a-b)b]..._数学_嘉宾wan1
编辑: admin 2017-15-06
-
4
设a/b=x
就变成1-1/x
第一个<号
令f(x)=lnx+1/x-1
求导1/x-1/x^2=1/x(1-1/x)>0
所以f(x)递增 最小值是f(1)=0 所以f(x)>0 第一个<成立
第二个<号
令f(x)=x-1-lnx
求导1-1/x>0 递增 f(1)=0 所以f(x)>0 第二个<成立
微分中值定理
令f(x)=lnx f'(x)=1/x
由拉格朗日中值定理
存在b
lna-lnb=1/c*(a-b) 那么ln(a/b)=1/c*(a-b)
其中b 令:(a/b)=t得: 1-tb>0,lnt>0,t>1,所以上式成立. 2、lnt lnt+1 t1时)永远小于函数e^(t-1) 设a/b=x 就变成1-1/x0 第一个0 第二个 ln(b/a)-2(b-a)/(b+a) =ln(b/a)-2(b+a-2a)/(b+a) =ln(b/a)-2+4a/(b+a) =ln(b/a)+4/[(b/a)+1]-2 令b/a=x 因为0题1:
【a>b>0,证明(a-b)/a】[数学科目]
题2:
【◆微积分证明设f(x)在[a,b]连续,在(a,b)可导,f(a)=0...】[数学科目]
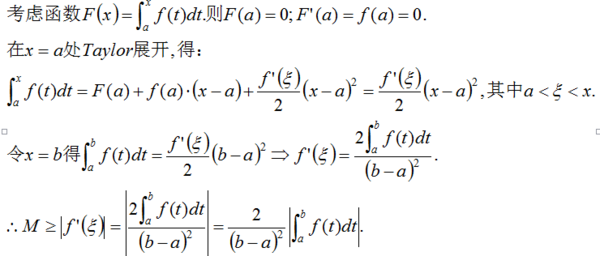
题3:
【设a>b>0,证明(a-b)/a要求用微分中值定理证明】[数学科目]
题4:
大一微积分作业设f(x)=a+x^2,x0,x=0处连续,试确定a和b的值[数学科目]

题5:
设0[数学科目]
